亲爱的读者，你是否曾在数学的世界里迷失方向，被那些复杂的公式和定理搞得头昏脑胀？今天，我要带你走进一个神奇的世界，那里有一个名叫欧拉函数的数学小精灵，它可是数学界的大明星呢！

一、欧拉函数的诞生之谜

欧拉函数，又称欧拉φ函数，用符号φ(n)表示。它最初是由瑞士数学家欧拉在18世纪提出的。欧拉函数的诞生，源于他对数论的研究。当时，欧拉在研究一个有趣的问题：一个正整数n，它的正因数中，有多少个是质数？

为了解决这个问题，欧拉提出了φ(n)的概念。简单来说，φ(n)就是小于或等于n的所有正整数中，与n互质的数的个数。互质，就是指两个数的最大公约数为1。比如，φ(6)等于2，因为6的因数有1、2、3、6，其中与6互质的数有1和5。

二、欧拉函数的神奇之处

欧拉函数虽然简单，但它却有着许多神奇的性质。下面，就让我带你领略一下它的风采吧！

1. φ(n)的性质：φ(n)是一个正整数，且φ(1)=1。对于任意两个正整数m和n，如果它们互质，那么φ(mn)=φ(m)φ(n)。

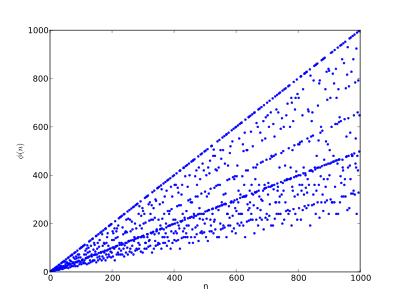
2. φ(n)的周期性：对于任意正整数n，φ(n)的值在n的范围内是有限的。这是因为，随着n的增加，与n互质的数的个数会逐渐减少，直到达到一个最小值。

3. φ(n)的分布规律：欧拉函数的值在n的范围内呈现出一定的分布规律。例如，当n为质数时，φ(n)=n-1；当n为合数时，φ(n)的值通常小于n。

三、欧拉函数的应用

欧拉函数在数学、计算机科学、密码学等领域都有着广泛的应用。以下是一些典型的应用场景：

1. 密码学：欧拉函数在密码学中有着重要的应用。例如，RSA加密算法就是基于欧拉函数的性质设计的。

2. 计算机科学：欧拉函数在计算机科学中也有着广泛的应用。例如，它可以用来优化算法，提高程序的运行效率。

3. 数学竞赛：欧拉函数是数学竞赛中常见的考点。掌握欧拉函数的性质，可以帮助你在竞赛中取得好成绩。

四、欧拉函数的挑战

虽然欧拉函数有着许多神奇的性质和应用，但它也有一些挑战。以下是一些关于欧拉函数的挑战：

1. 计算φ(n)：对于较大的n，计算φ(n)的值可能比较困难。因此，如何快速计算φ(n)是一个值得研究的课题。

2. 寻找互质数：在寻找与n互质的数时，如何高效地找到这些数也是一个挑战。

3. 欧拉函数的推广：欧拉函数可以推广到更广泛的数学领域，如数论、组合数学等。如何将这些推广应用于实际问题，是一个值得探索的方向。

亲爱的读者，通过这篇文章，你是否对欧拉函数有了更深入的了解呢？这个神奇的数学小精灵，不仅让我们领略了数学的魅力，还为我们带来了许多实际应用。让我们一起，继续探索数学的奥秘吧！